什么是机器学习?
个人理解:
机器在已有数据集的基础上进行学习,并抽象成数学模型,通过训练模型进行预测或分析,从而解决现实中的问题
机器学习的分类
监督学习
我们给定数据集,并且给定“正确答案”,机器需要学习“正确答案”的计算方法
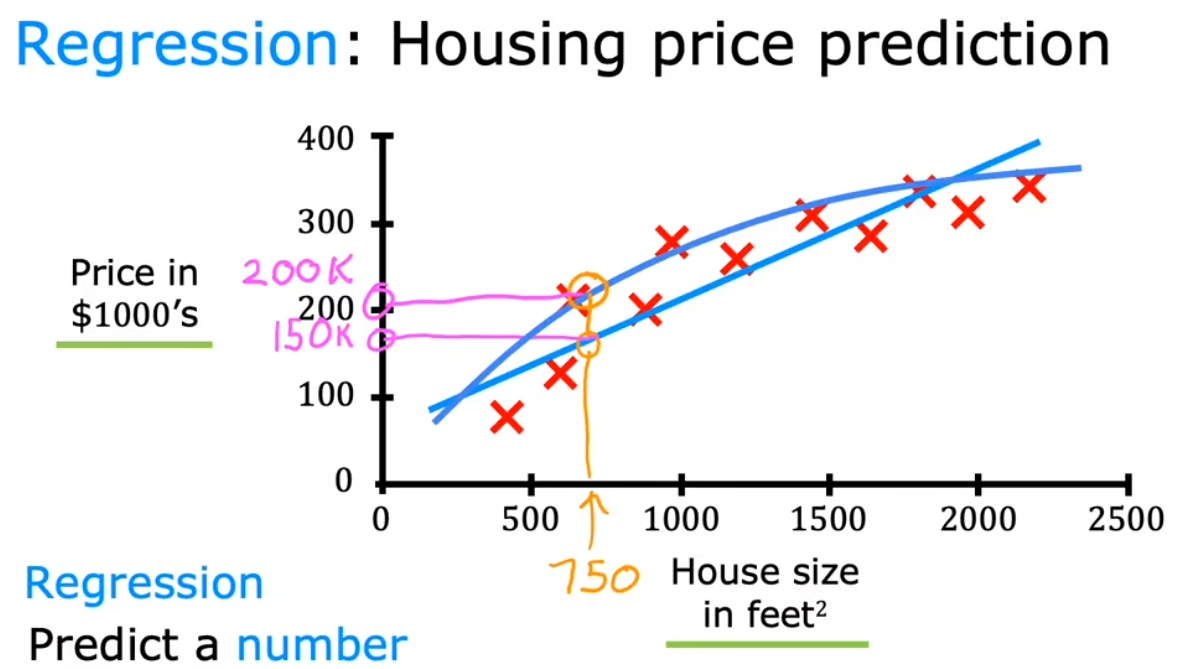
回归(Regression)
本质是两者的映射关系:
输入 x —–> 期望输出 y
通过学习已有数据,得出合理的预测结果
常见应用场景:语音转文本、文本翻译、图片识别
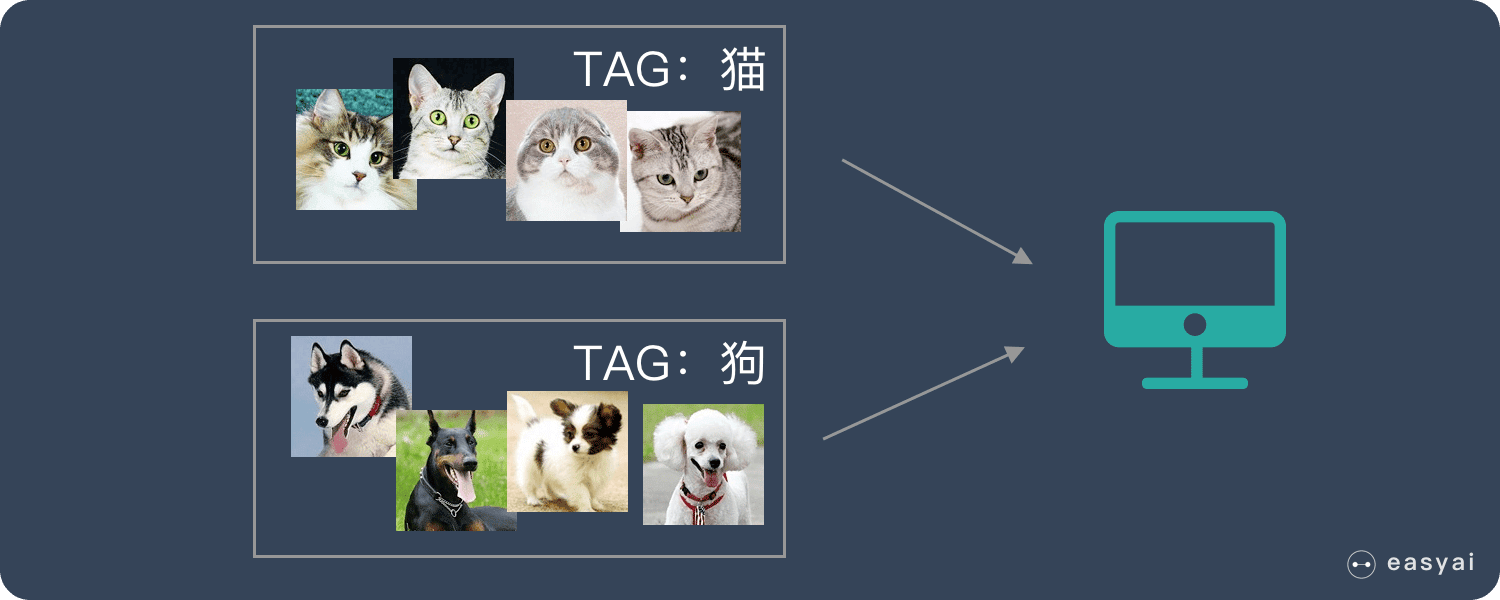
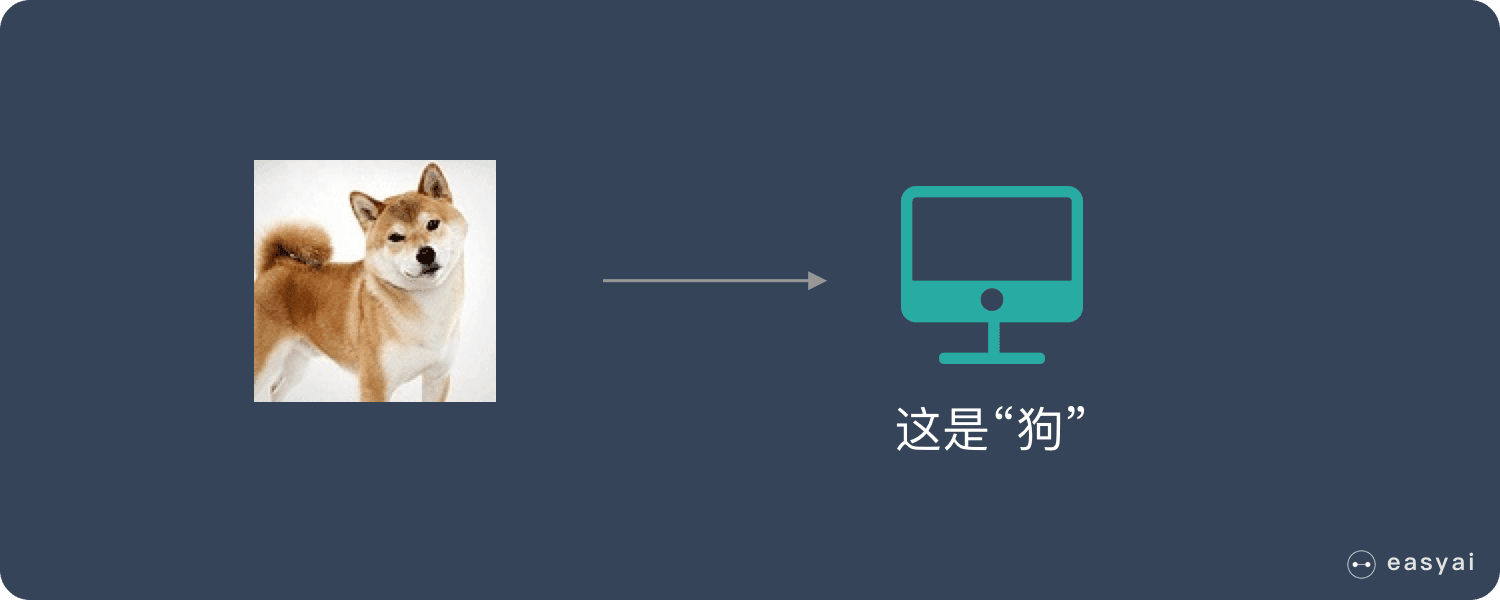
分类(Classification)
给定机器一系列猫和狗的图片,并给这些图片打上标签(即“正确答案”),机器通过大量的学习,能够对一张新照片识别出是猫还是狗
非监督学习
给定 x,不给定 y
给定的数据集没有“正确答案”,所有的数据都不知道具体类型,无监督学习需要挖掘出潜在的特征、结构等
聚类(Clustering)
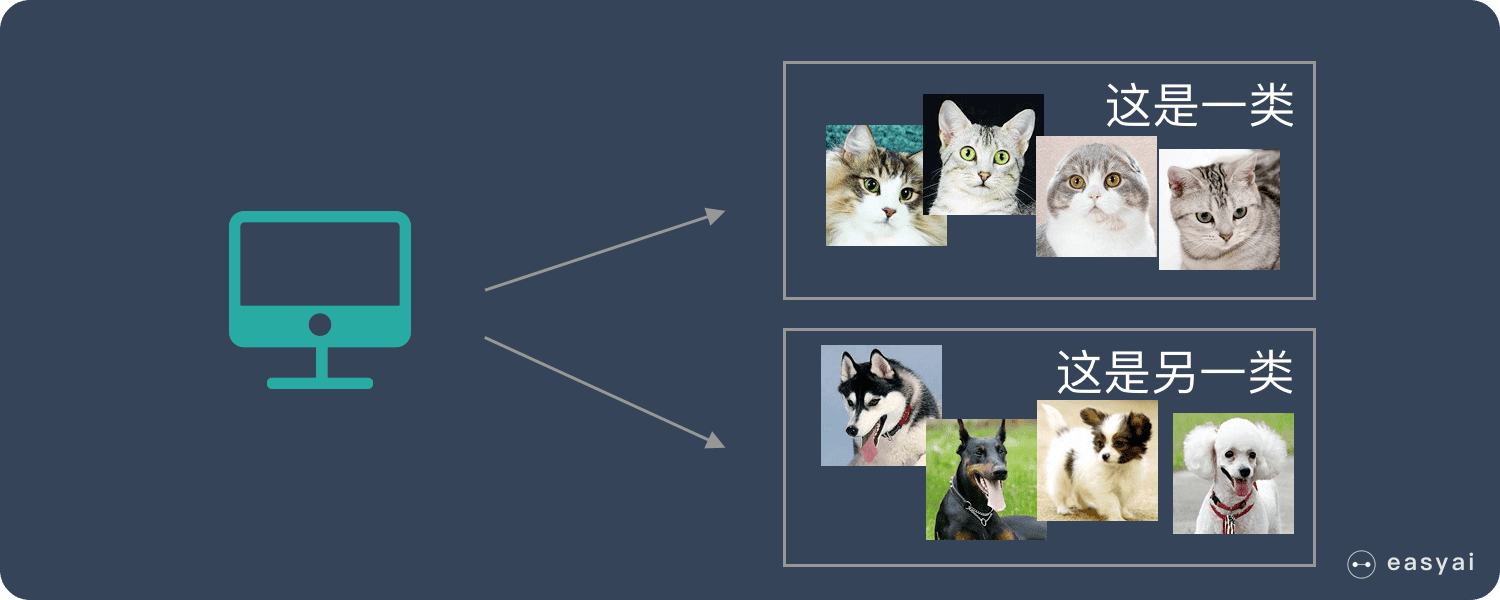
把一些猫和狗的照片给机器,但不给这些照片打标签,机器需要自行对这些照片进行分类
通过学习,机器可以将这些照片分为两类,但机器并不知道哪个是猫,哪个是狗,对机器来说只知道是AB两类

异常检测(Anomaly detection)
降维(Dimensionality reduction)
线性回归
代价函数(Cost Function)
代价函数是用于衡量预测值与真值之间误差的一种函数

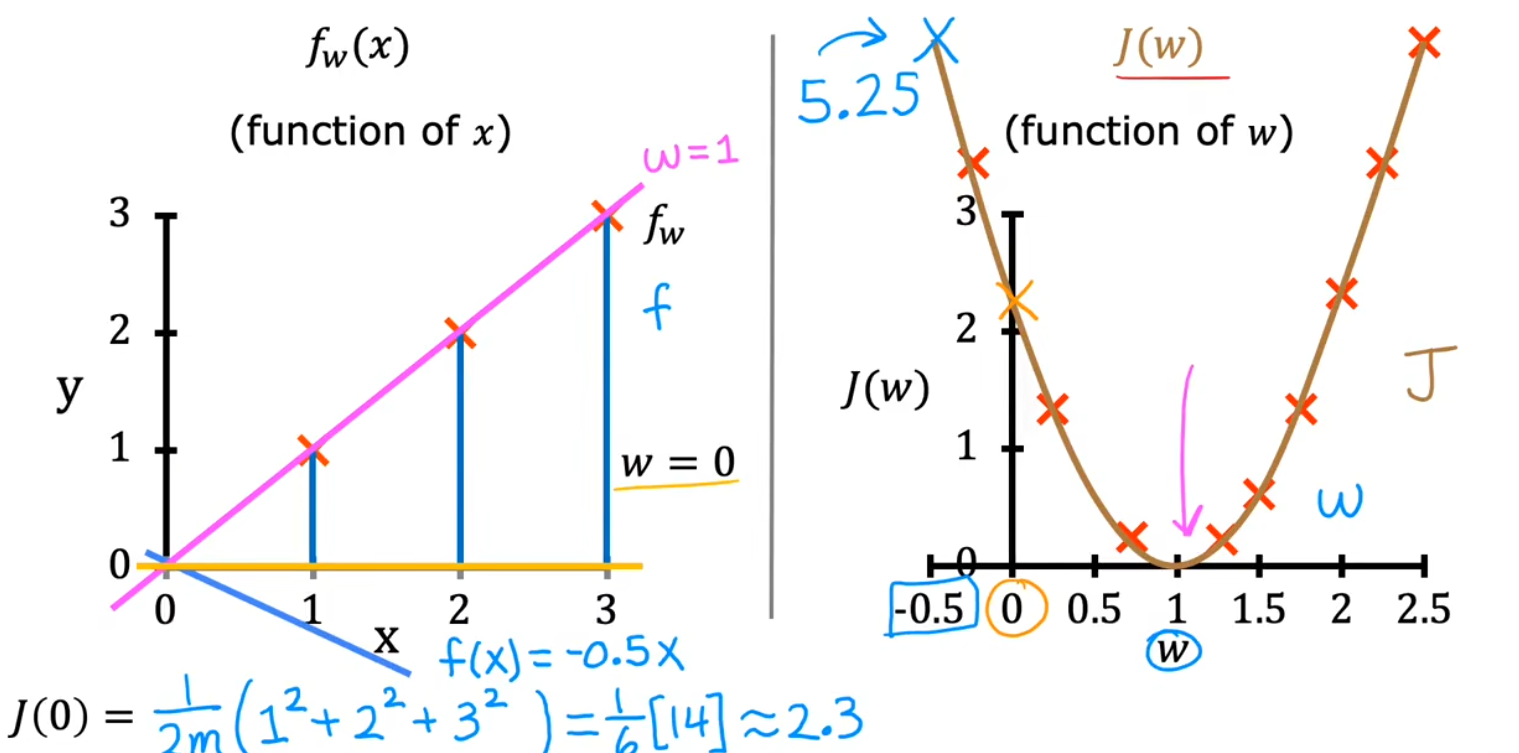
梯度下降
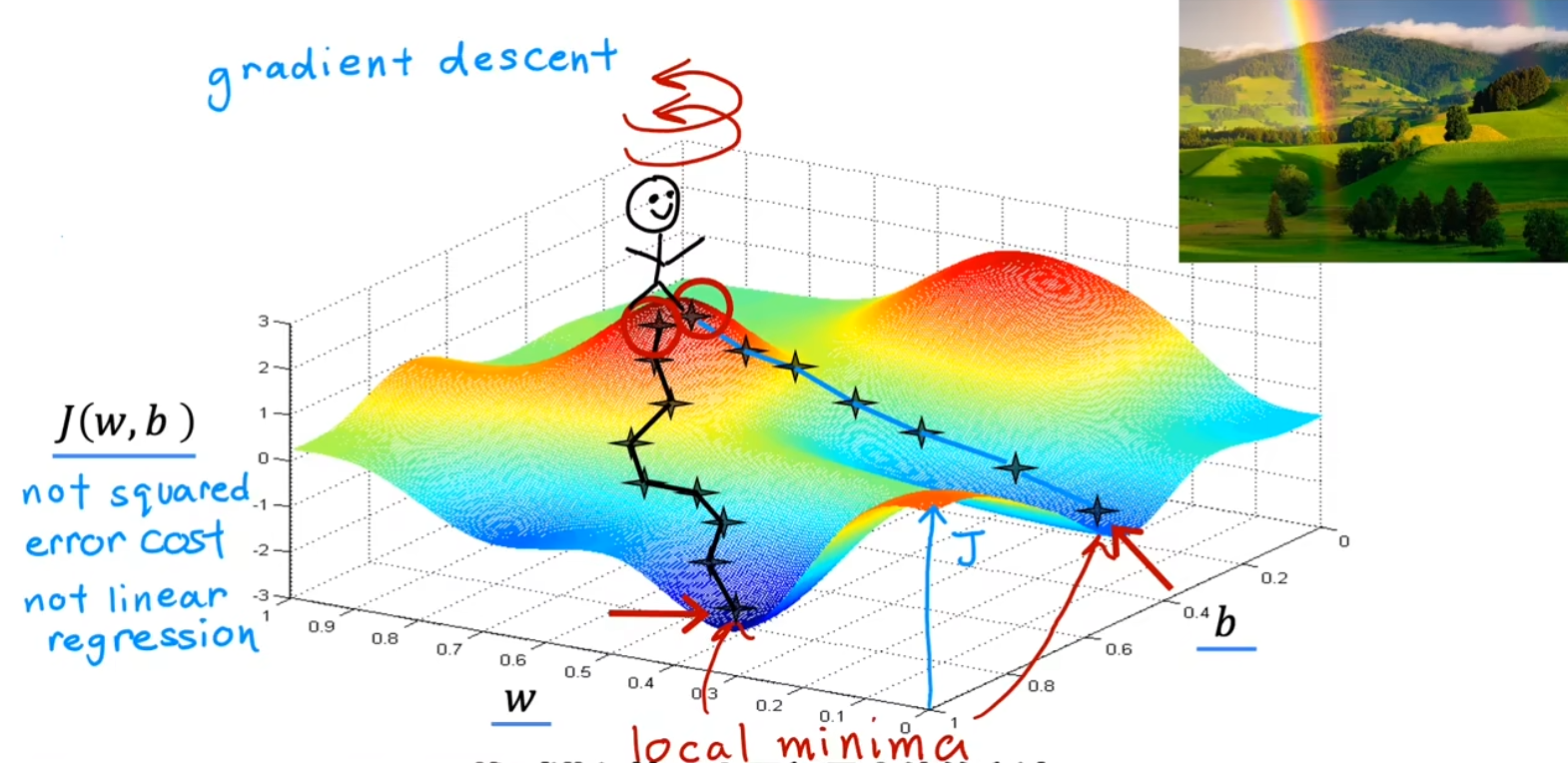
目的是找到 J(w,b) 中,函数最小值 Jmin 对应的参数值(以上图只含一个参数的 f(w) 和 J(w) 为例,即抛物线最低点的 w 值)
梯度下降公式
α 为学习率,取值越小,调整的幅度越小,取值越大,调整的幅度越大
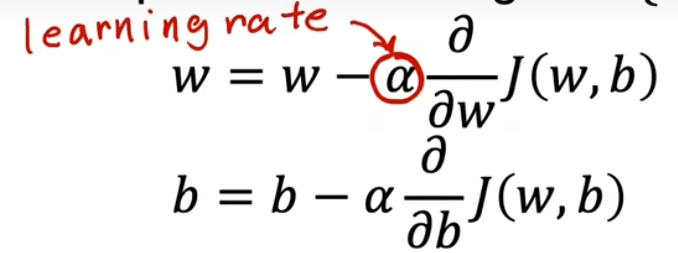
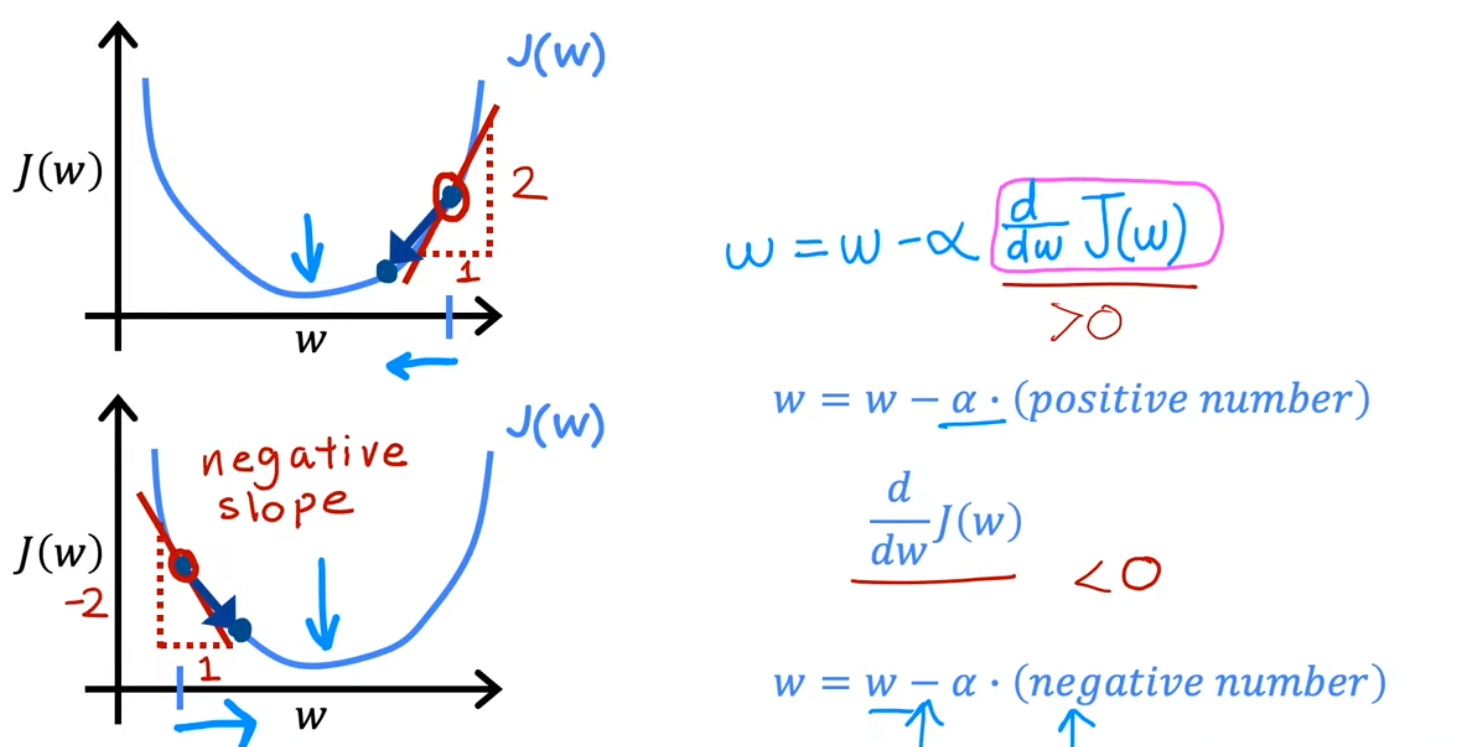
小细节:在实际应用中,w,b 更新应为同步更新,如左图

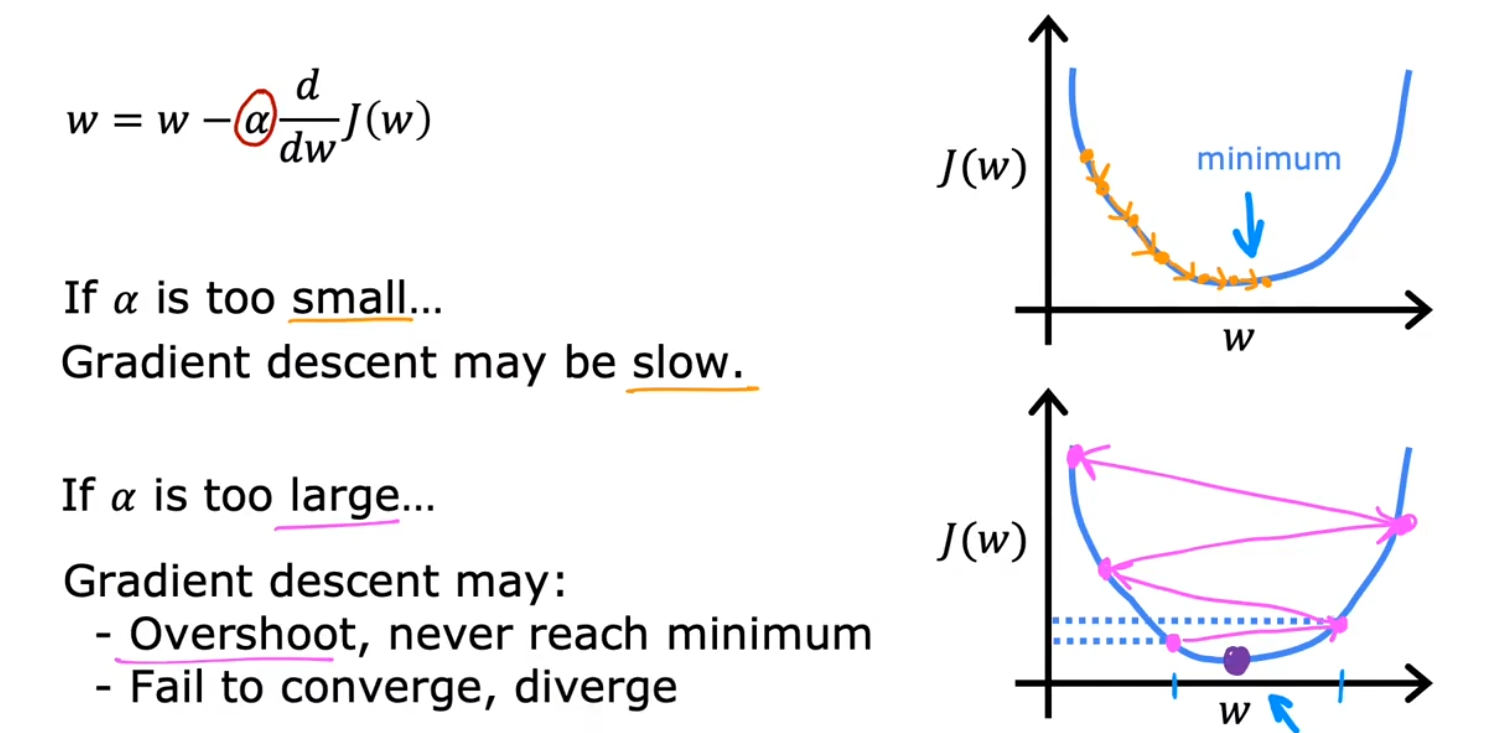
学习率 α
一个非常小的正数,但过大、过小都会导致问题
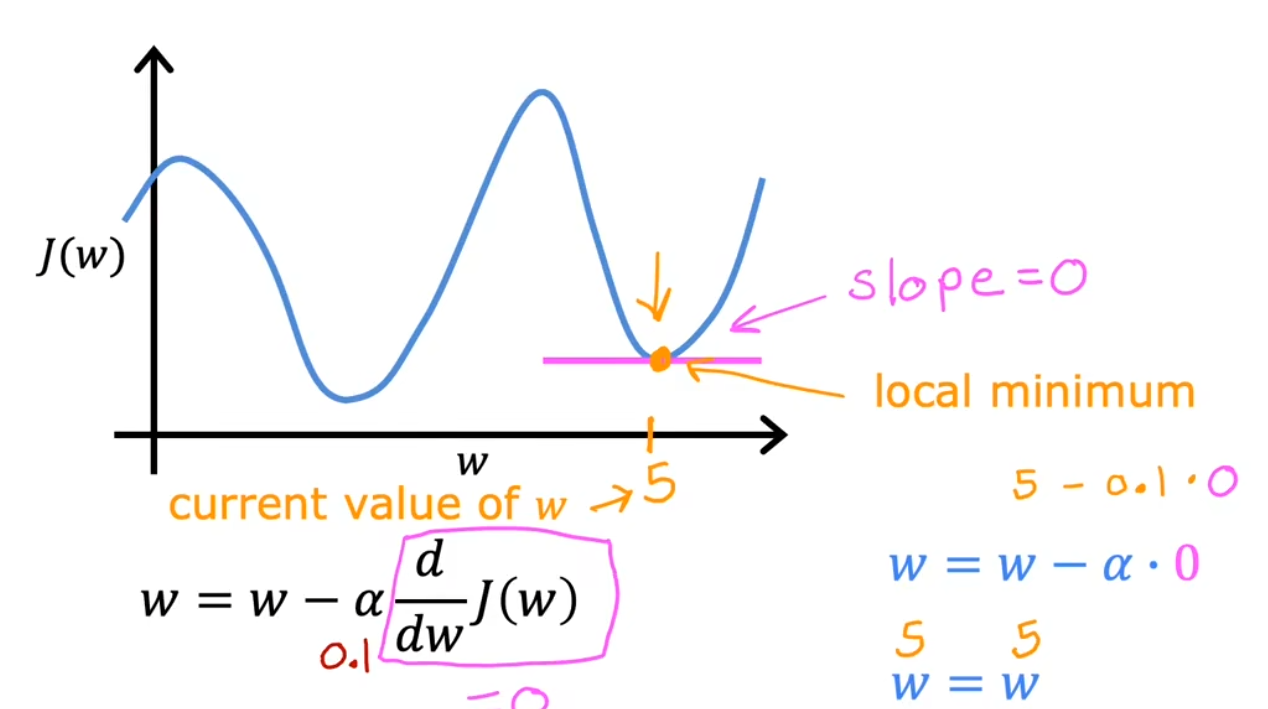
局部最小值
如果参数已经调整至局部最小值,算法将不再更新参数,即不会继续找真实的极小值
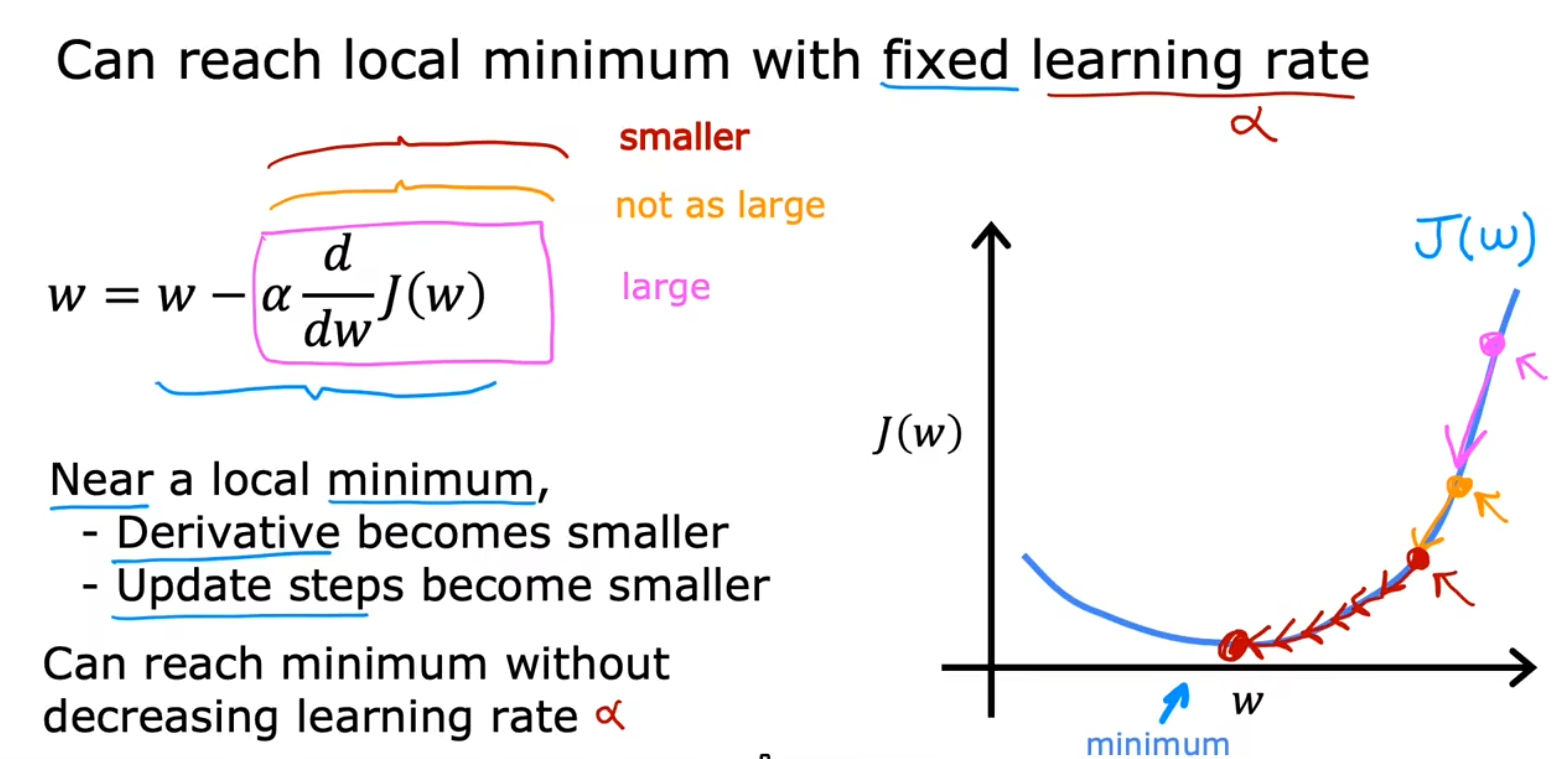
接近局部最小值
当算法逐步接近最小值时,调整的幅度也会逐渐减小,因为导数值也在不断变小
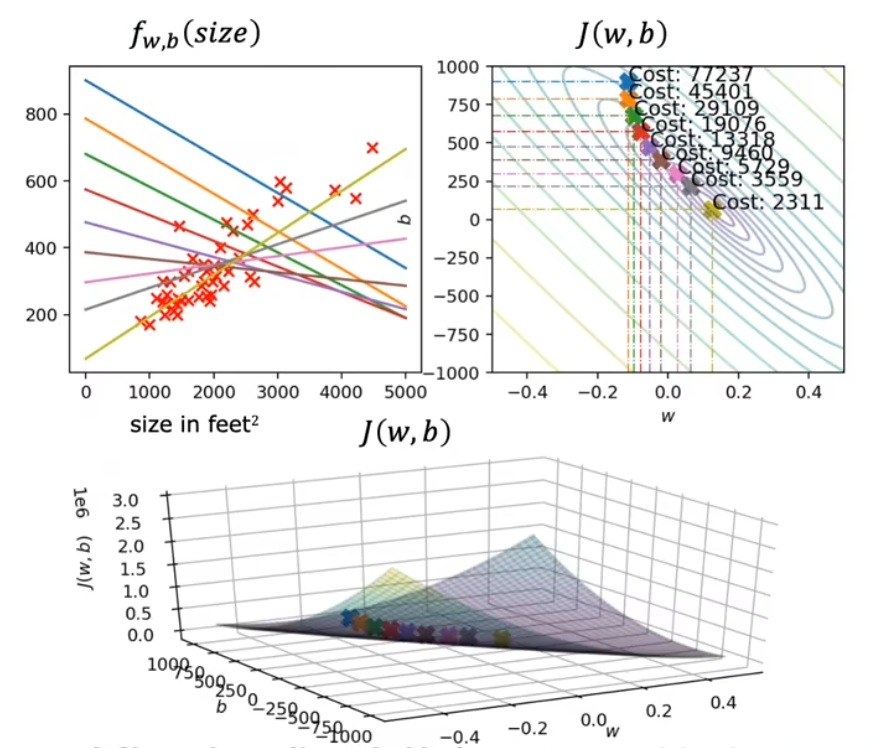
实际应用
随着梯度下降算法的进行,函数 f 由最上方蓝色调整至最下方黄绿色,更好地拟合了数据
多维特征
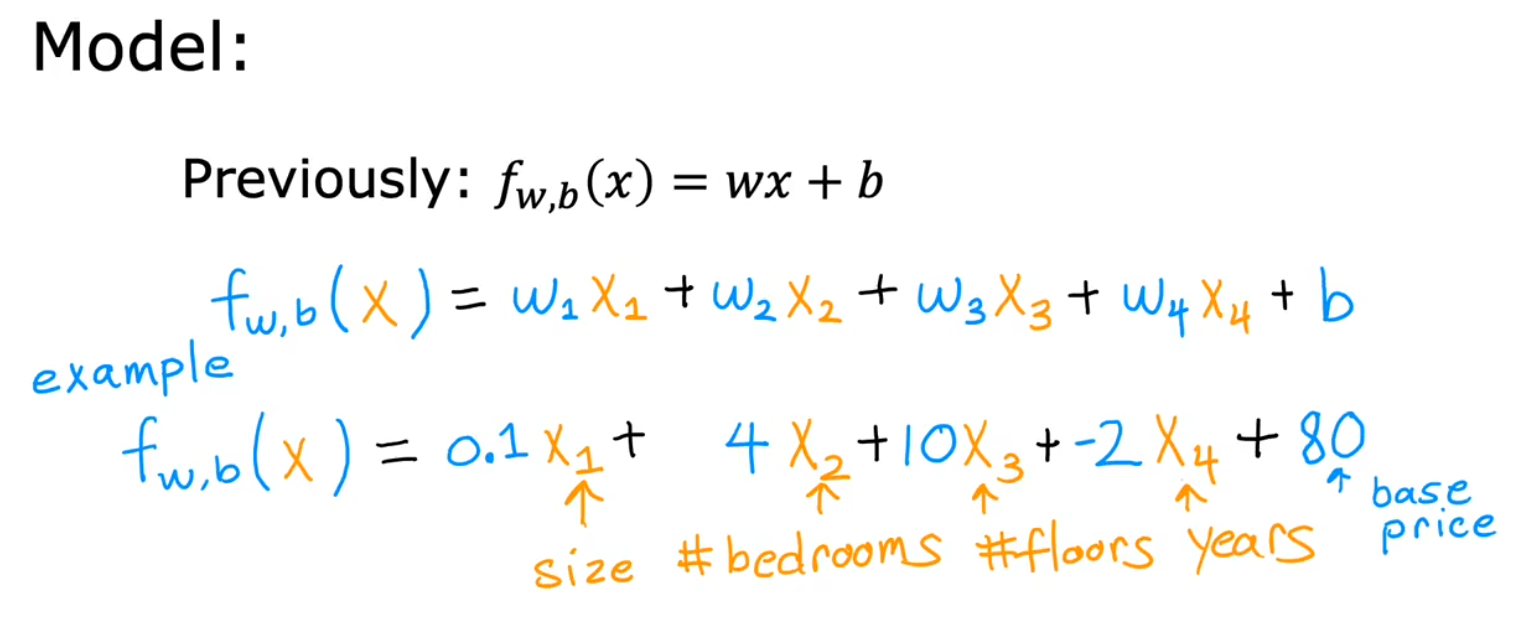
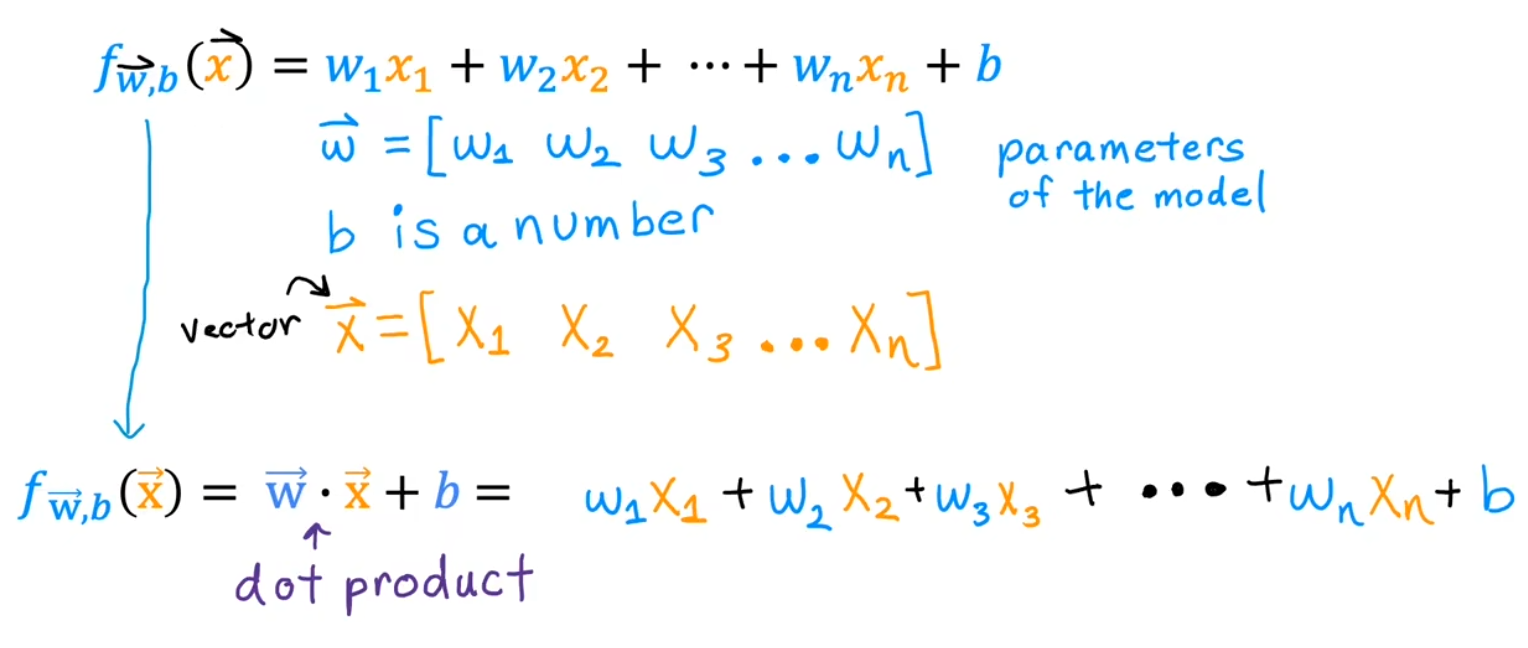
向量化的好处
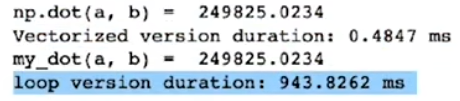
向量化不仅使代码更加简洁,还能使运算更快

原因是计算机底层硬件对向量运算有更好的优化支持,可以并行(in parallel)计算多条数据
而传统的 for 循环则需要一个个计算结果
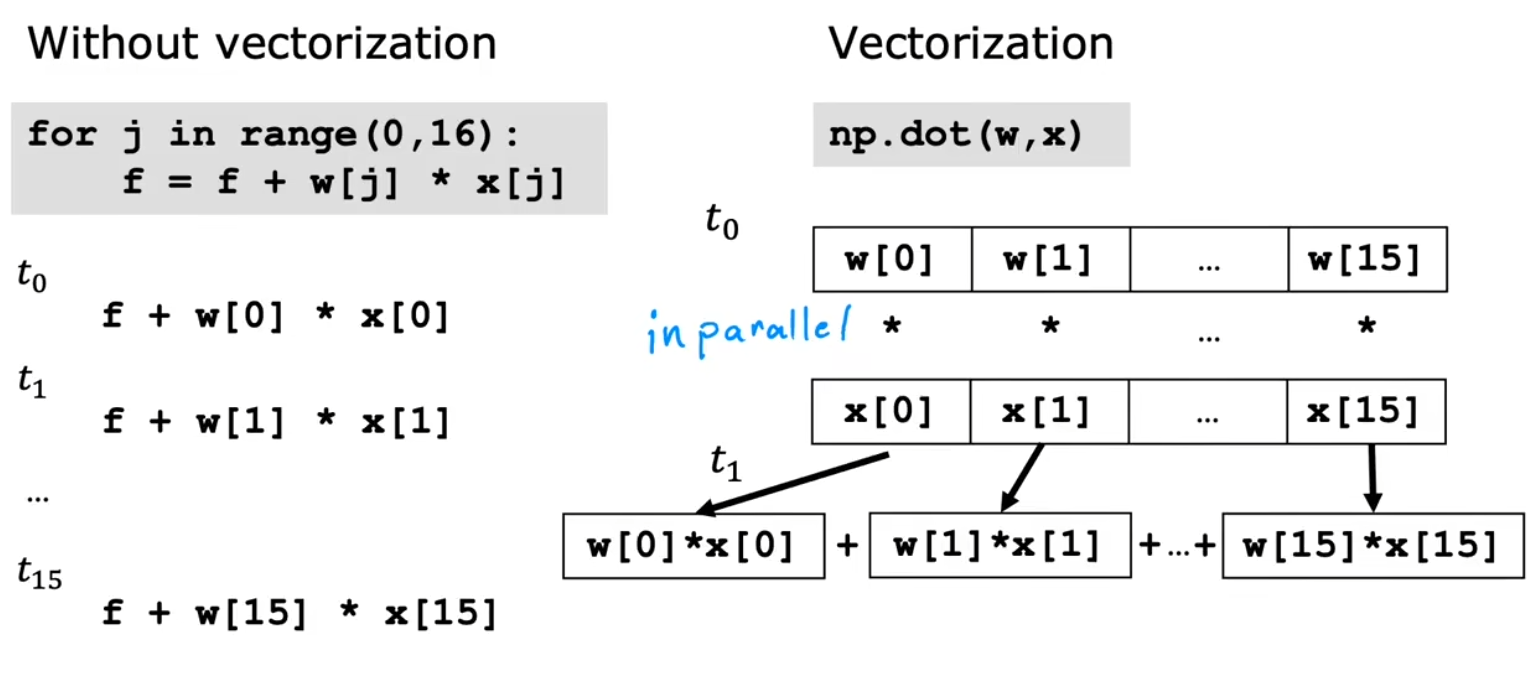
使用向量化和不使用向量化的时间对比:
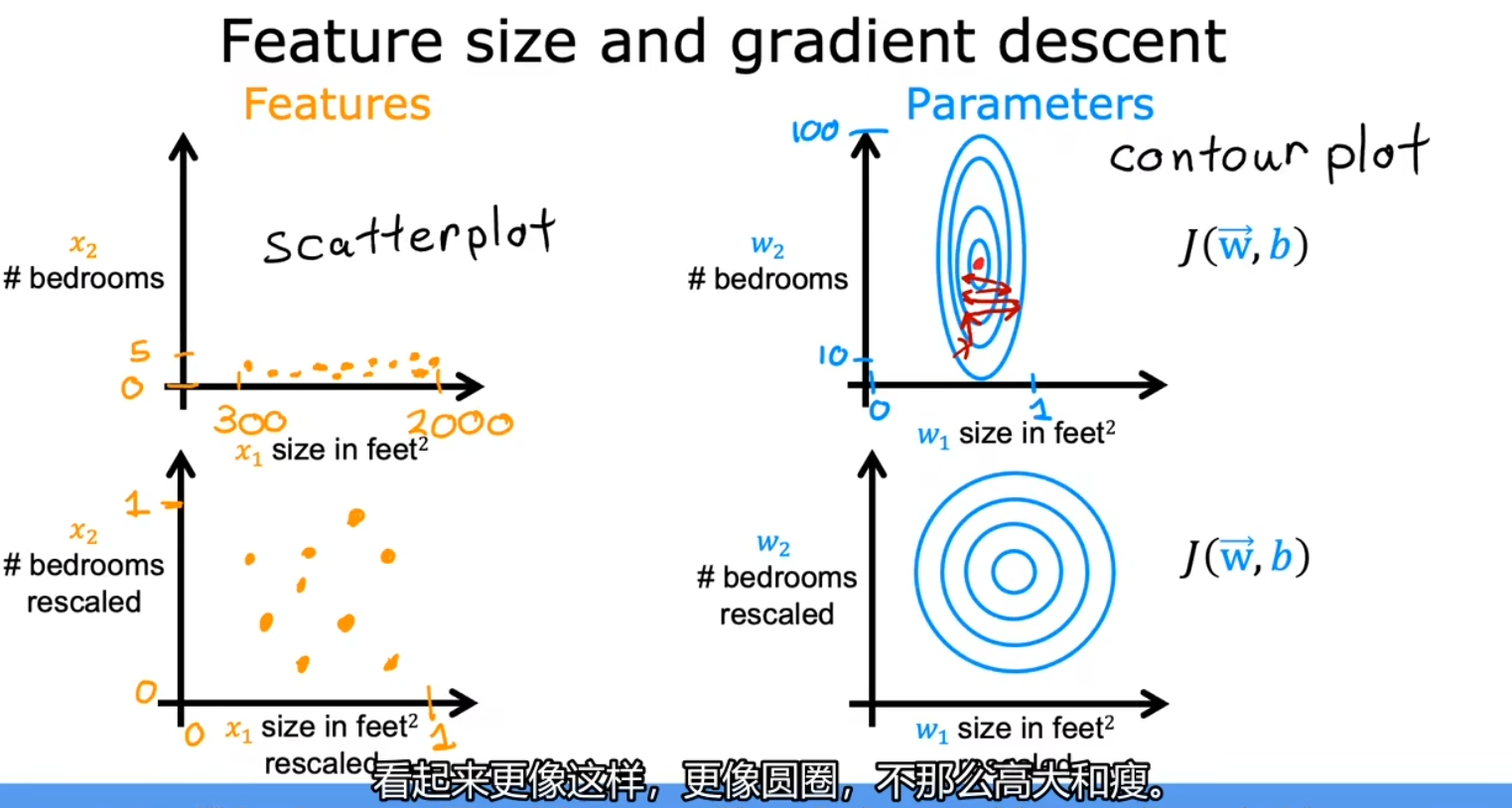
特征缩放
目的是使梯度下降运行得更快,将所有特征值缩放到同一个相似的范围,如 (-1, 1) 之间

法一:除以最大值

法二:均值归一化

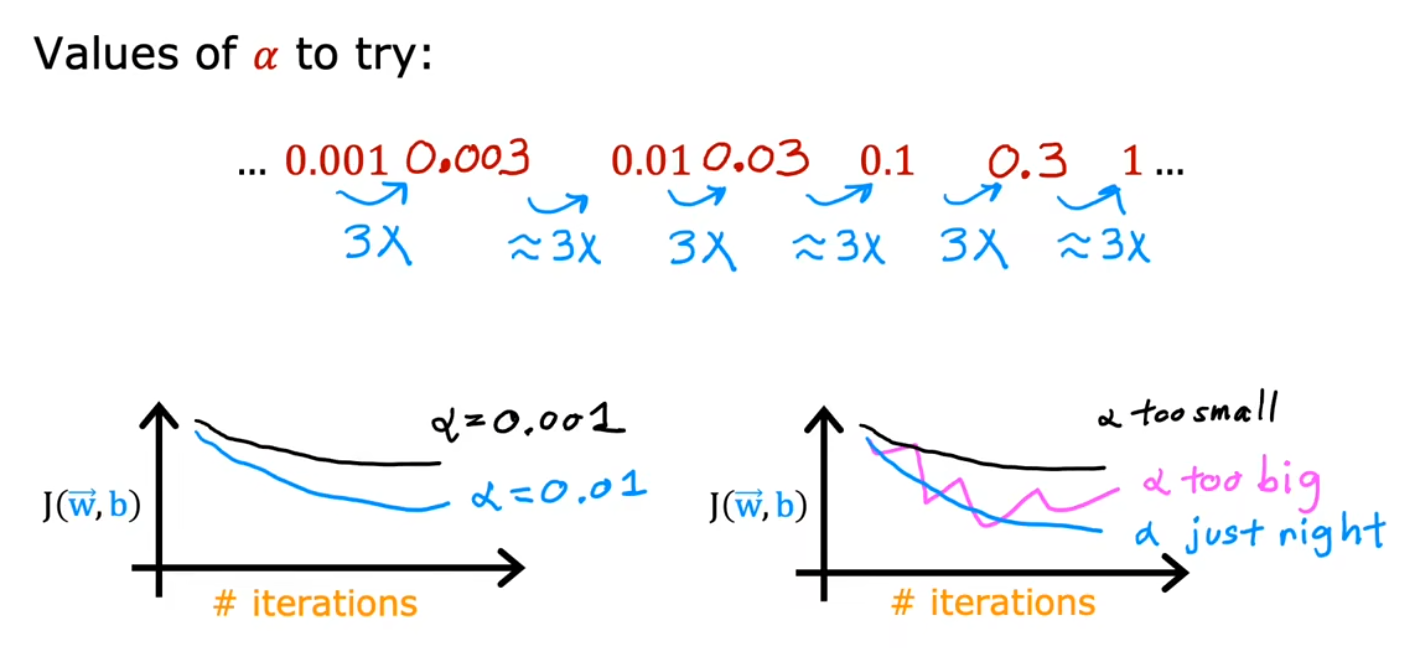
迭代次数和学习曲线
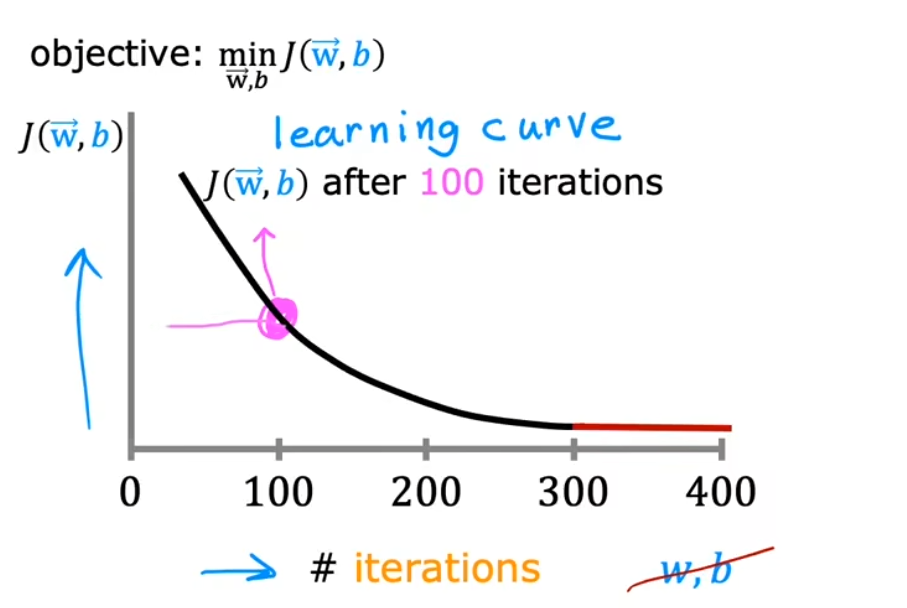
学习率 α 的取值
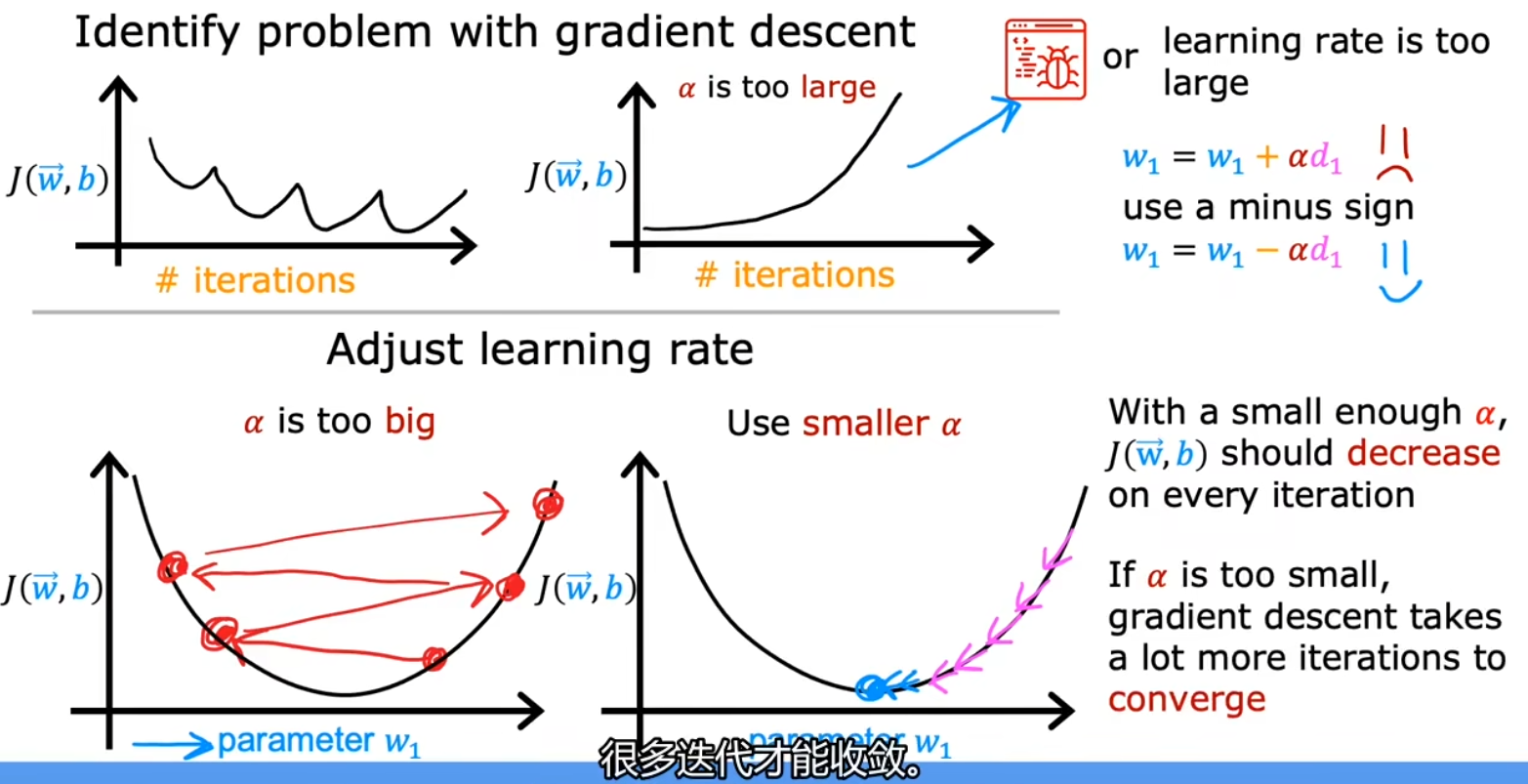
逻辑回归
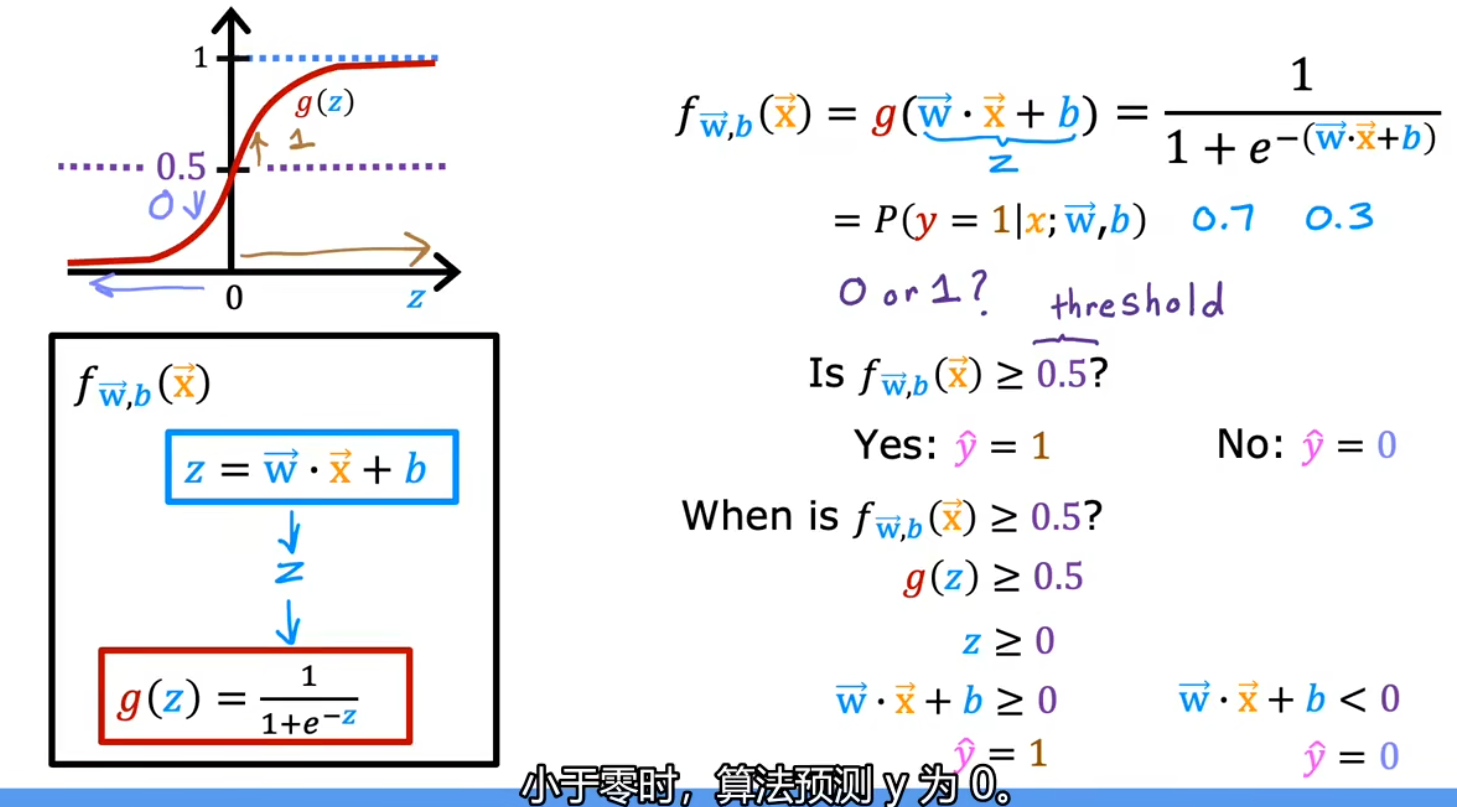
虽然含有回归(Regression)一词,但实际上是用于分类(Classification)的
与线性回归不同,逻辑回归输出的结果只能是 0(false, no)或 1 (true, yes)

线性回归的局限性
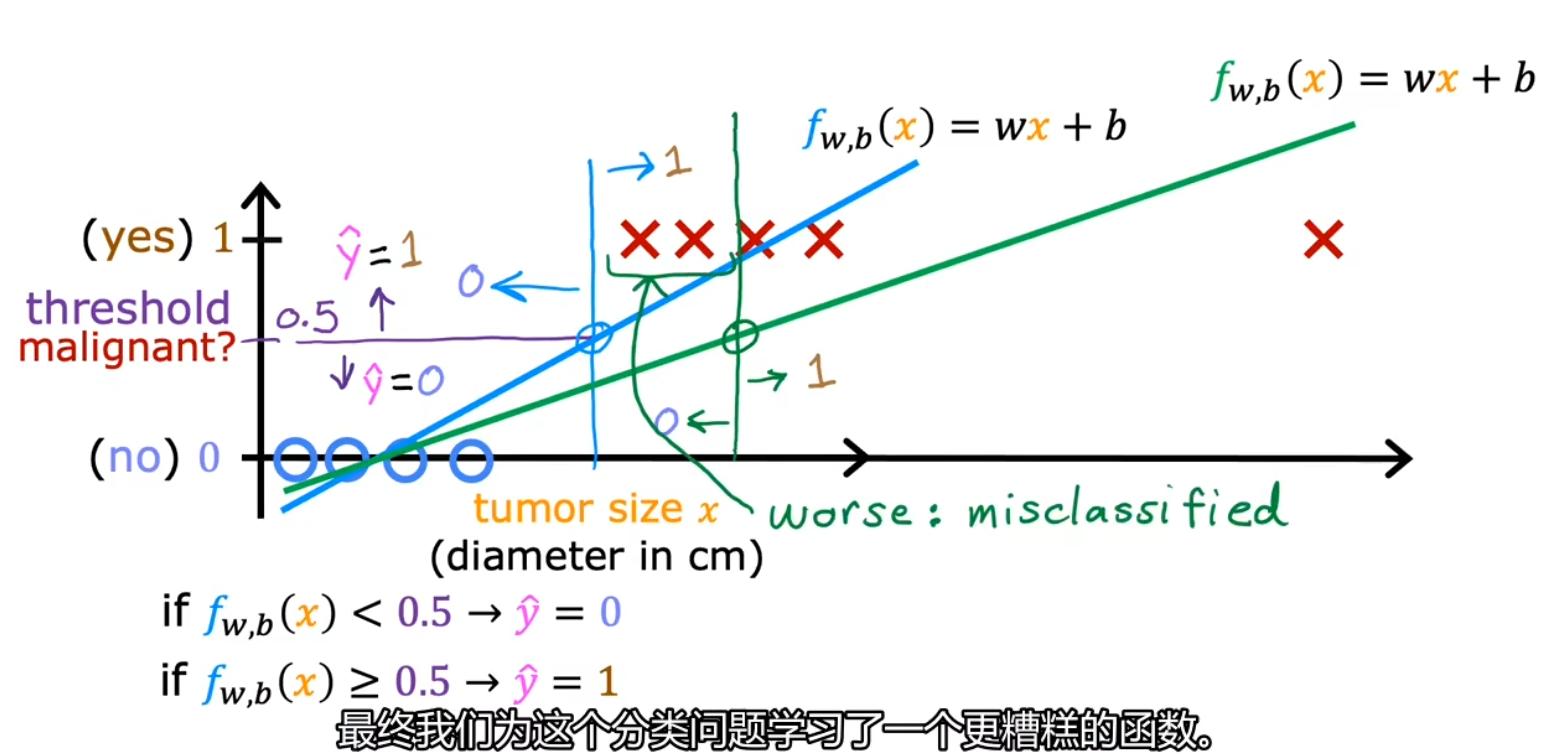
决策边界
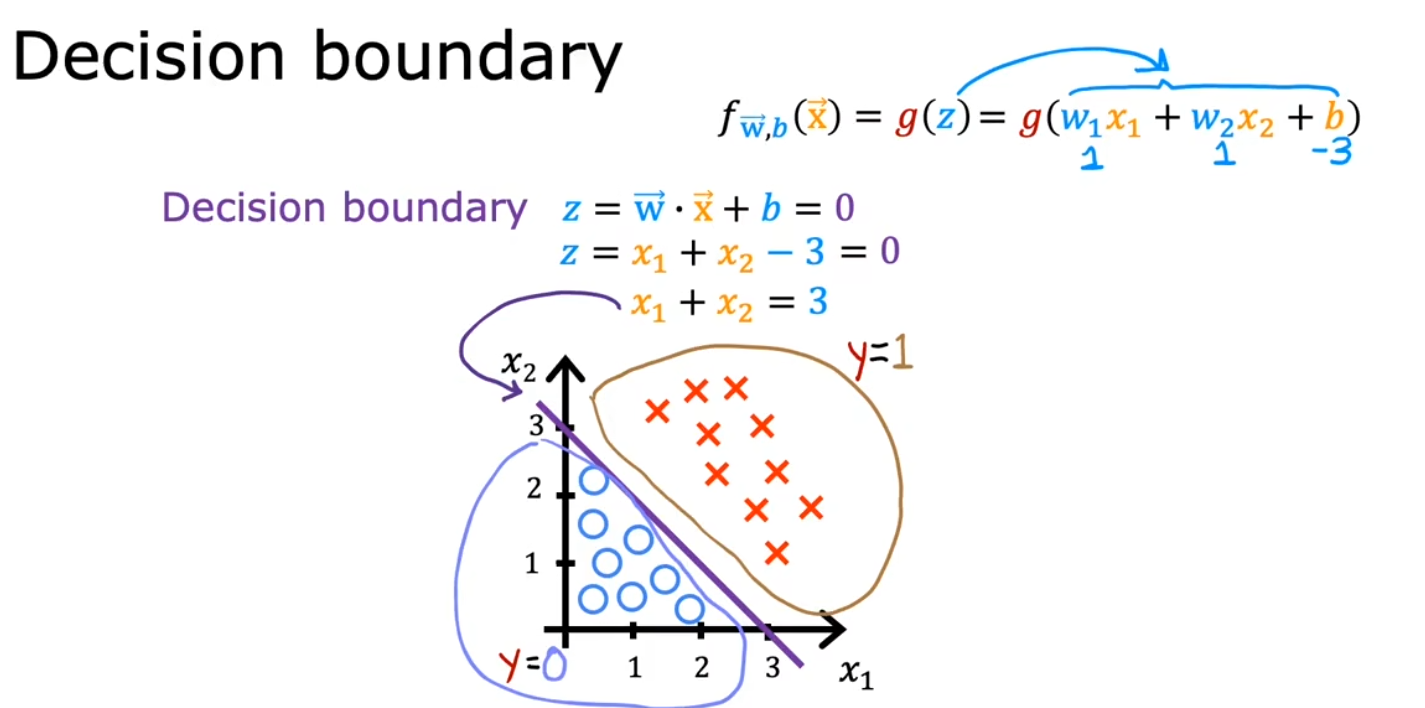

逻辑回归的代价函数
损失函数( L 函数)
用于衡量单个训练数据的误差,作为定义代价函数的基础
输出 y 为 1 时:
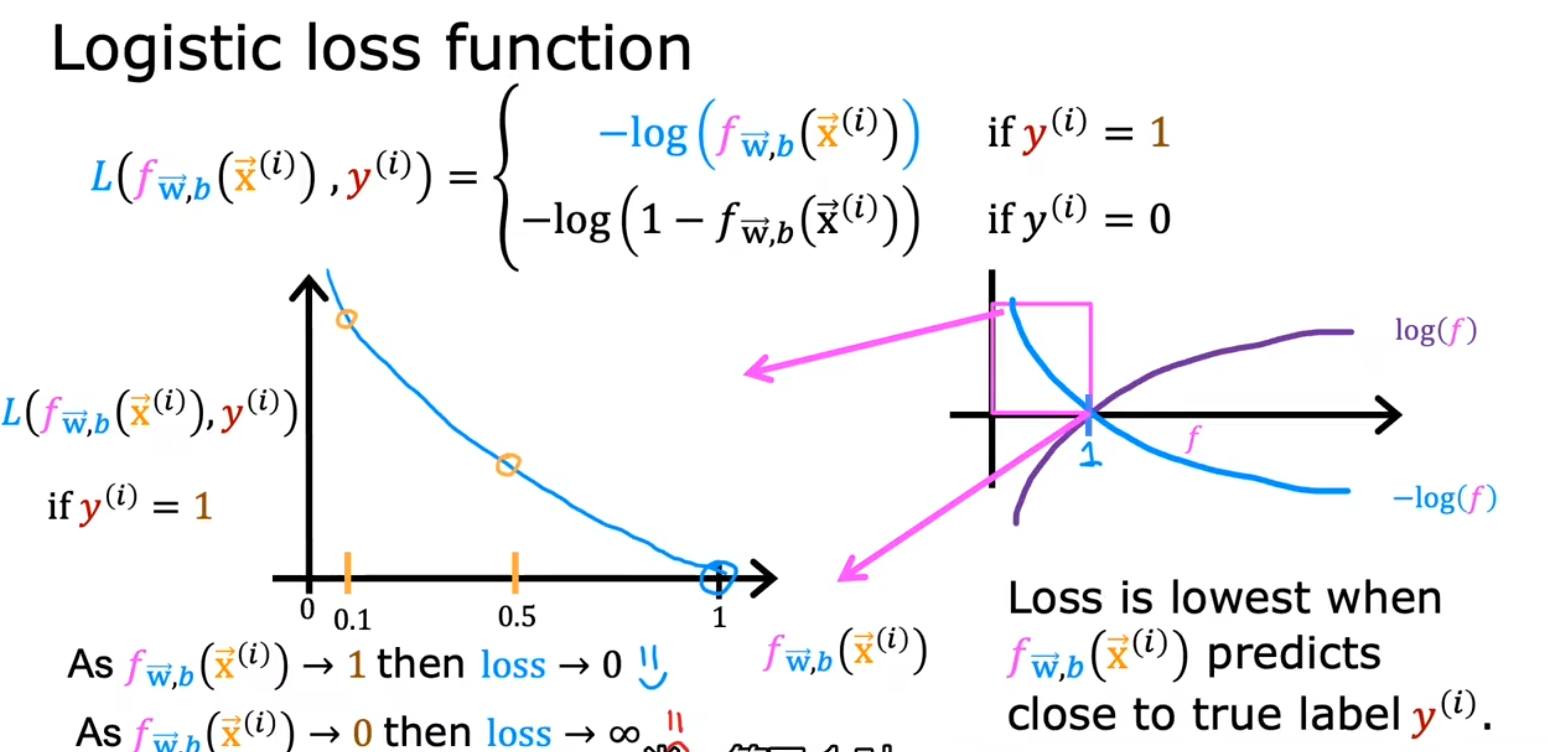
输出 y 为 0 时:
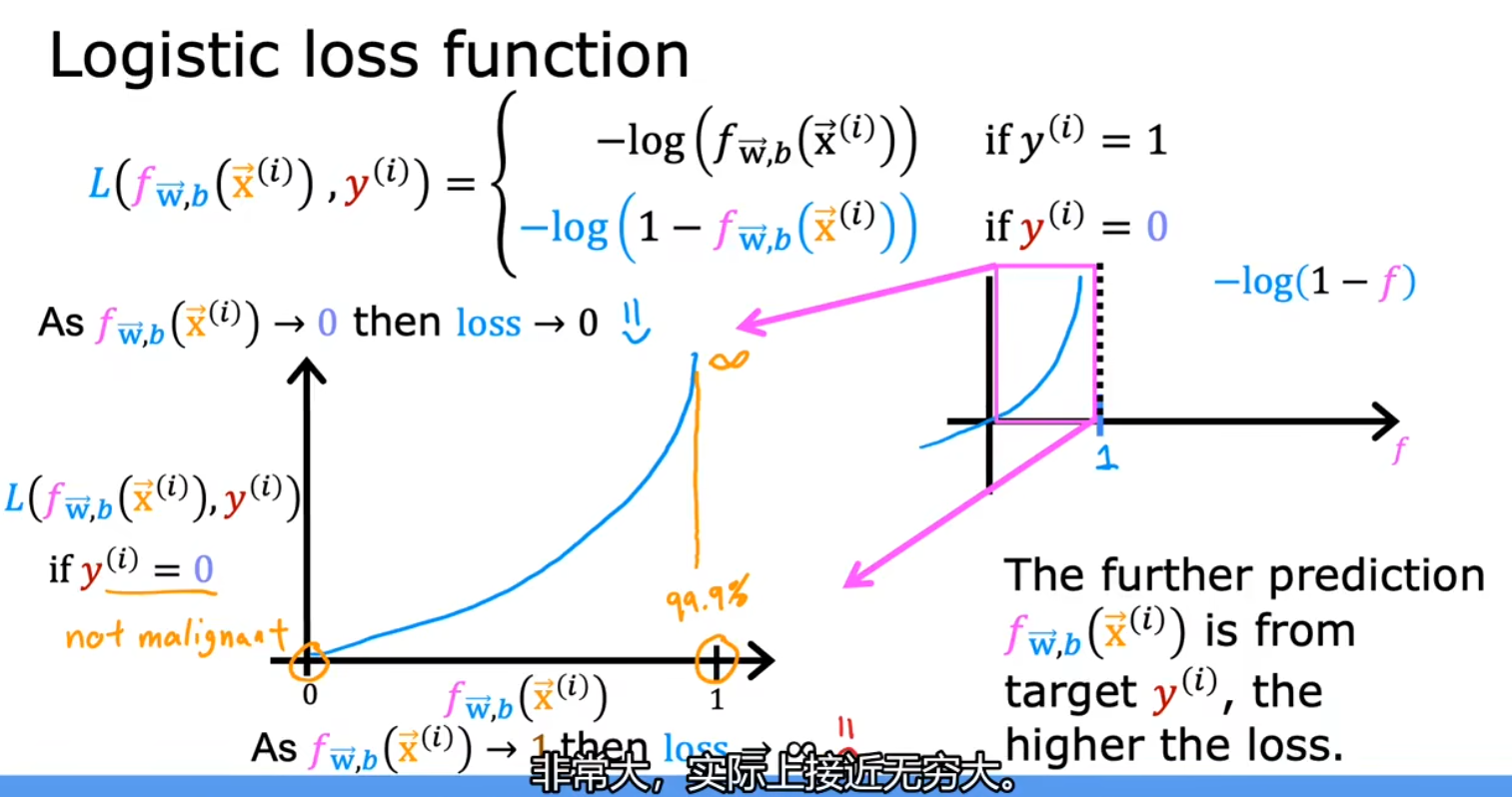
代价函数( J 函数)
用于衡量整个训练集的误差

逻辑回归的梯度下降
公式看上去和线性回归一样,但 f 函数的定义不同

欠拟合、过拟合
左:欠拟合
右:过拟合
中:正好合适
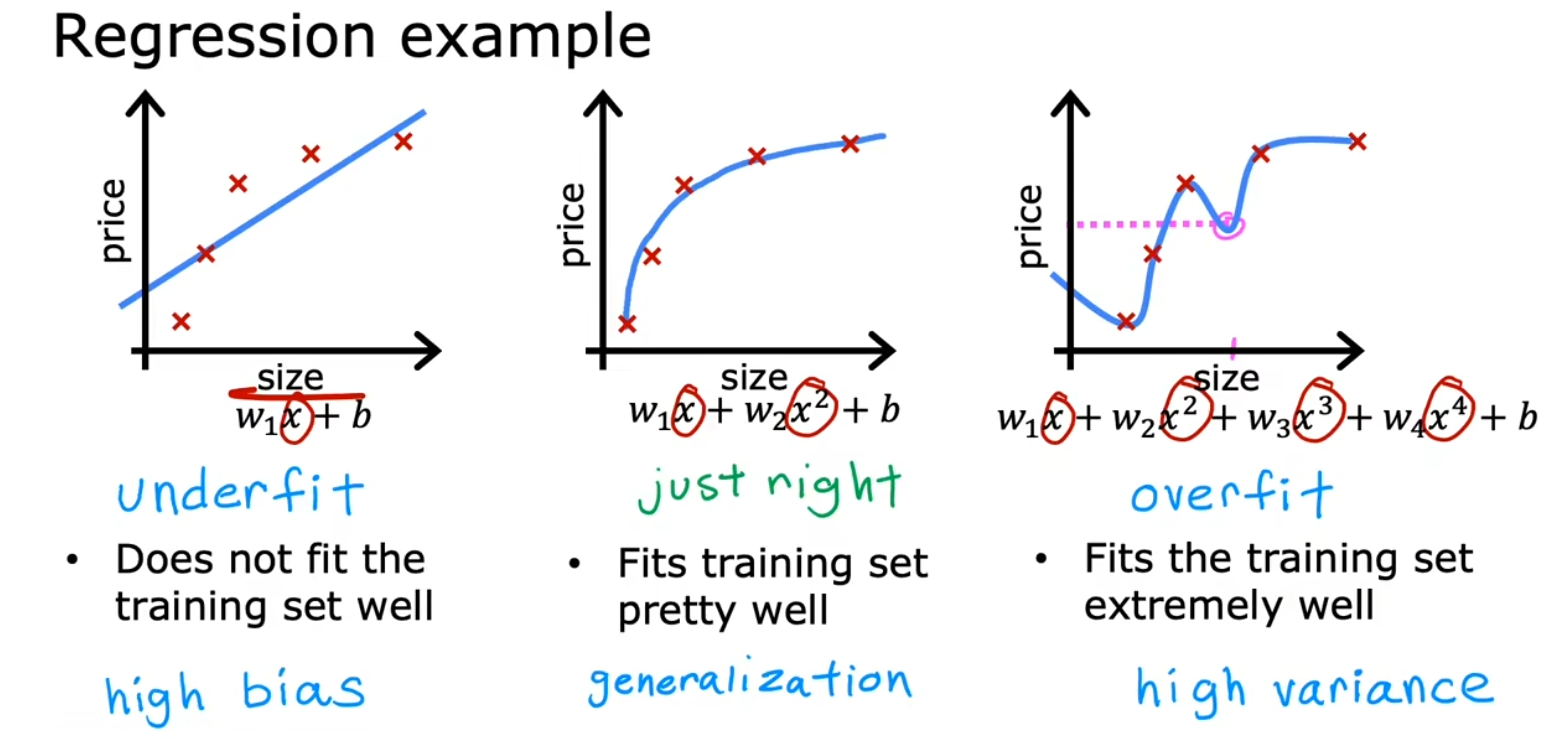
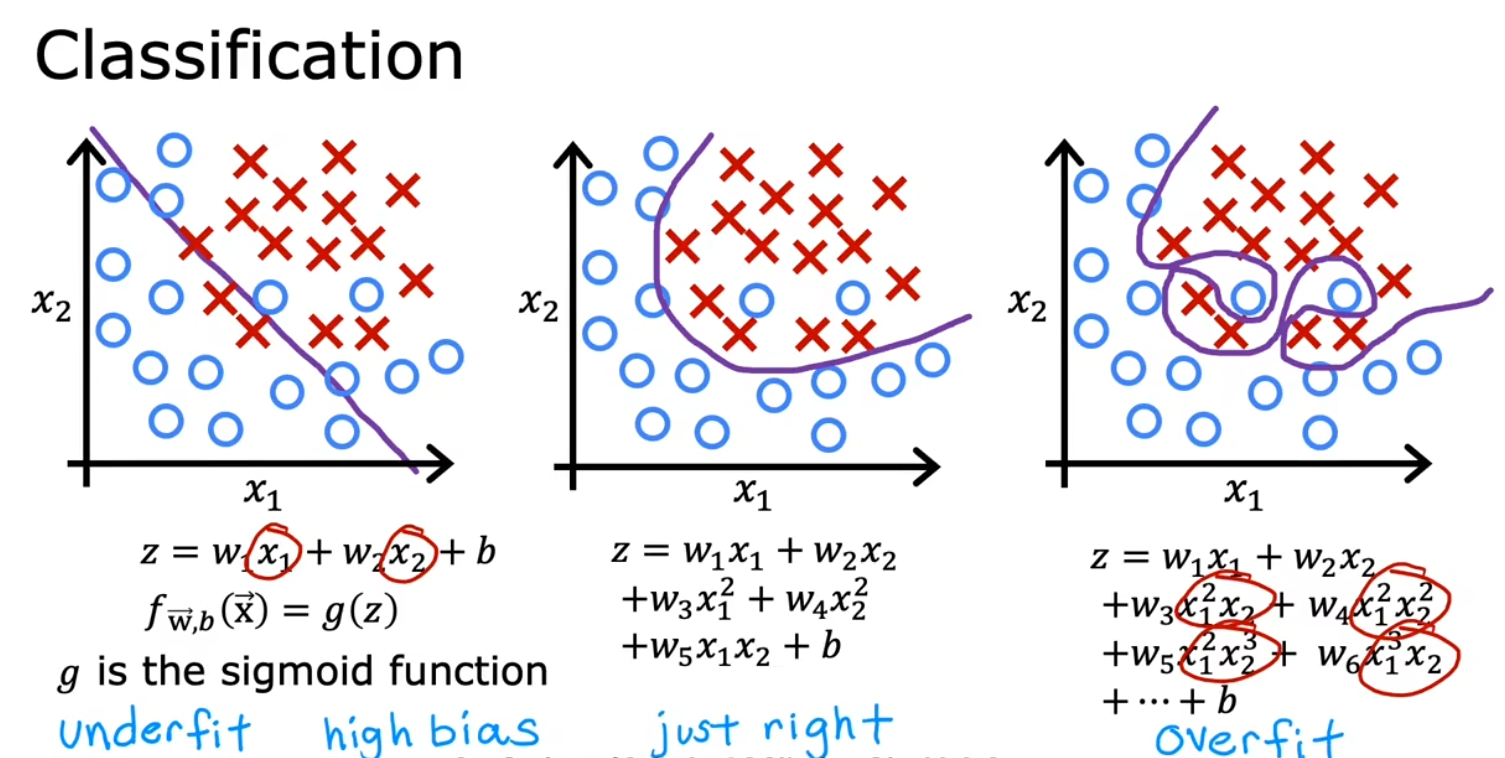
欠拟合
又被称为高偏差,模型对训练数据的拟合度不足
过拟合
又被称为高方差,模型对训练数据拟合很好(甚至可以无误差),但泛化能力不足,测试数据表现很差
解决过拟合
- 收集更多训练数据
- 若训练数据不多,则减少特征数,但可能导致有用的特征丢失
- 正则化,最常用的方法
正则化
正则化系数 λ 作用于代价函数 J(w, b),目的是减小某些参数 w(i) 的值,从而防止过拟合
下方右图紫线为正则化后得到的合适曲线

注意,λ 取值范围可以是 (0, +∞),但实际应用时需要设置为一个合理的值
过低,如设为 0,则正则化失效,仍是过拟合
过高,则参数 w 失效,J(w,b) = b,为一条直线,变为欠拟合

- Post link: http://example.com/2023/03/28/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0/
- Copyright Notice: All articles in this blog are licensed under unless otherwise stated.